Can skinfold thickness equations be substituted for bioimpedance analysis in children?

Abstract

Objective

The aim of the present study was to evaluate the agreement between the most used skinfold thickness equations with multi-frequency bioimpedance analysis in the prediction of body fat levels in children.

Method

A cross-sectional study of healthy Brazilian community-dwelling individuals. The anthropometric assessment included height, body mass, arm circumference, and waist circumference. The percentage of body fat was obtained by measuring skinfold thickness equations and using bioimpedance analysis, and skinfold thickness was measured using a scientific skinfold caliper. Bland–Altman plot analysis was used to verify the agreement between the methods.

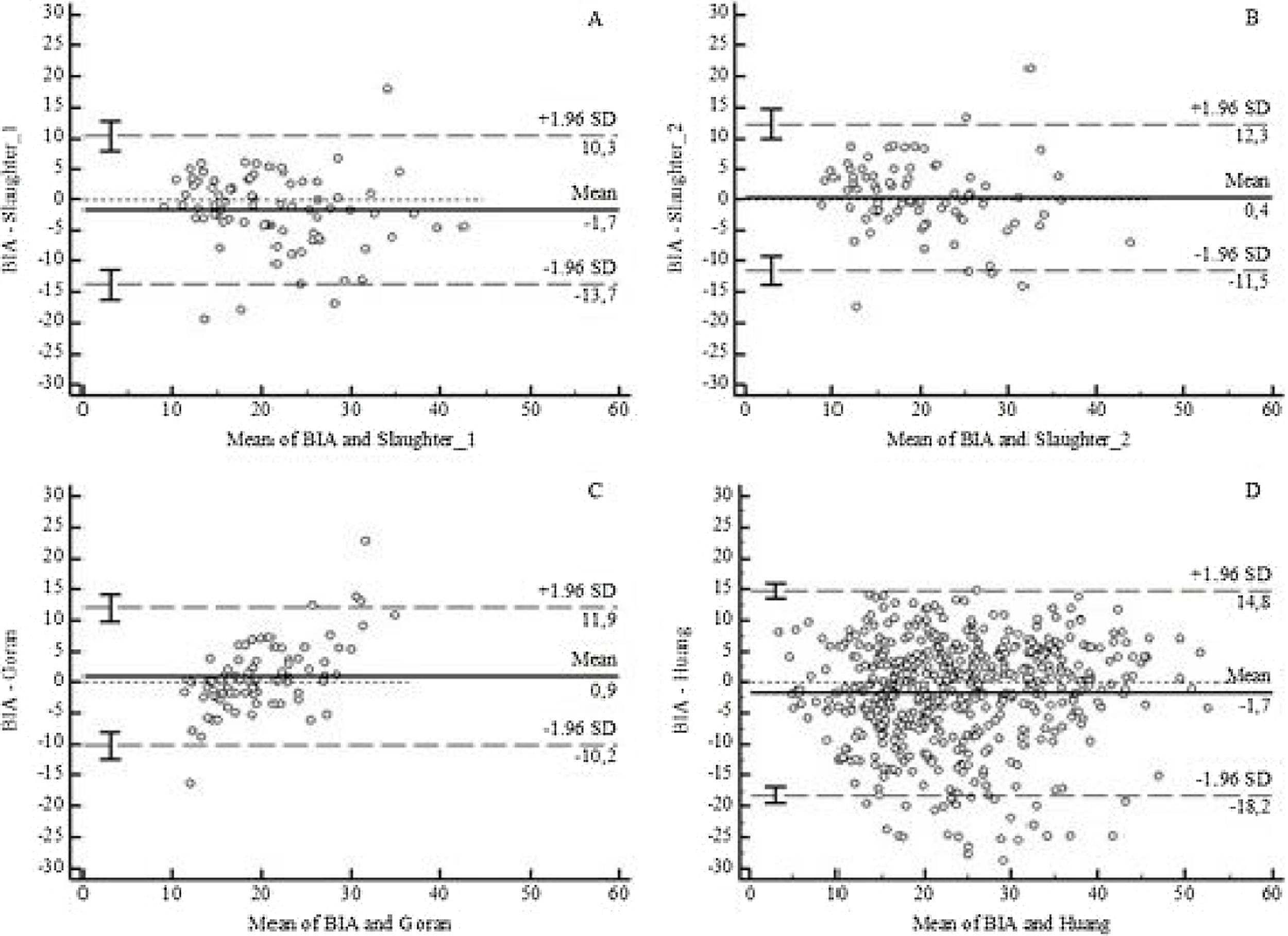
Results

There were 439 children and adolescents evaluated, with a mean age of 11.6 ± 3.7 years. The mean body fat by bioimpedance analysis was 22.8% ± 10.4%, compared to 22.4% ± 8.8% by Slaughter (1), 20.4% ± 9.2% by Slaughter (2), 19.6% ± 4.4% by Goran, and 24.7% ± 10.0% by Huang equations. Bland–Altman plot analysis revealed limits of agreement greater than 8% between the bioimpedance analysis approach and equations, exceeding the clinically acceptable limit predefined a priori. None of the equations had good agreement with bioimpedance analysis.

Conclusion

It was concluded that skinfold thickness and bioimpedance analysis should not be used interchangeably in children and adolescents.

Introduction

Overweight and obesity rates have risen at alarming rates worldwide.¹ Obesity is characterized by excessive body fat, which is the main cause of chronic non-transmissible diseases in adulthood.² Therefore, maintaining the recommended range of lean mass is one of the goals of treating these diseases. Thus, body composition analysis is attracting interest as a research and clinical analysis tool.³ However, isolated measures such as body mass index (BMI) and arm and waist circumferences can be inaccurate when used to predict total body fat mass.³

Body composition can be measured by a variety of techniques, and these methods vary in their cost, accuracy, feasibility, and sophistication.⁴ There is no direct method to measure adiposity, and the most common indirect methods are bioelectrical impedance analysis (BIA) and skinfolds thickness.^5–7 The greatest advantage of using this method is the low cost and feasibility of performing the exam.^8,9 Numerous equations have been developed to estimate body composition from anthropometry. Studies have identified a significant and moderate correlation between the percentage of body fat (%BF) measured by the skinfold thickness equations and BIA.^10–13 However, there is a lack of evidence on the agreement between BIA and standard skinfold equations and, therefore, whether they can be used interchangeably in children and adolescents.

The aim of the present study was to evaluate the agreement between the most used skinfold thickness equations with multi-frequency BIA in the prediction of body fat levels in children. The hypothesis was that standard anthropometric methods and BIA can be used interchangeably.

Methods

The present cross-sectional study followed the guidelines for writing observational articles STROBE Statement.¹⁴

Setting and participants

Healthy children and adolescents (5–18 years old) were recruited for convenience. Participants were considered if they had not been diagnosed with any chronic disease or were not on continuous medication. Exclusion criteria were contraindications to BIA, such as diseases affecting the electrical resistance of the skin, pregnancy, persons with an implanted pacemaker or cardioverter-defibrillator, and persons with amputation or using prosthesis/orthosis.

Participants were considered healthy if they had not been diagnosed with any chronic disease or were on continuous medication.

Data were collected from December 2015 to February 2018 in public and private schools, companies, and events in the cities of Southern Brazil. Recruitment occurred through word of mouth.

Data measurements

Anthropometric measurements included height, body mass, arm circumference, and waist circumference, following international standards for anthropometric assessment.¹⁵ Height was assessed using a metal stadiometer (Cescorf, Brazil) affixed on a vertical bar with an adjustable headpiece. The individuals were instructed to stand barefoot, arms along the body, and head in the Frankfort horizontal plane. Weight was assessed using a calibrated digital scale (Charder MS6121 model – Brazil) with a capacity of 200 kg and accuracy of 100 g, with as little clothing as possible, without shoes, and with no metal objects on the body. Body mass index (kg/m²) was then calculated. Arm circumference was measured at the midpoint between of the superior lateral edge of the acromial process, adjusted in the lateral deltoid position, viewed from the side, and from the proximal and lateral edge of the radius head.¹⁵ After marking, the midpoint was determined, and the perimeter of the relaxed right arm was measured. Waist circumference was defined at the minimum circumference between the iliac crest and the rib cage.¹⁶

The percentage of body fat was obtained by measuring skinfold thickness and applying equations, and by using multi-frequency BIA, which estimates body composition based on the different conductivities of the various tissues.

Skinfold thickness was measured using a scientific skinfold thickness caliper (Cescorf – Porto Alegre, Brazil). The assessment was done by one of two physical educators that are certified to at least level 1 of the International Society for the Advancement of Kinanthropometry (ISAK). Three anatomical sites on the right side of the body (triceps, calf, and subscapularis) were measured (in mm) in triplicate. The arithmetic average of the three measurements was calculated to determine the anatomical point value. Skinfold thickness equations were applied as proposed by Slaughter et al.,¹⁷ Goran et al.,¹⁸ and Huang et al.,¹⁹ as described below:

Skinfolds thickness equations

Slaughter 1

Females: %BF = 0.610 (sum triceps and calf skinfolds) + 5.1

Males: %BF = 0.735 (sum triceps and calf skinfolds) + 1.0

Slaughter 2: For subjects with sum triceps and subscapular skinfolds >35 mm

Females: %BF = 0.546 (sum of triceps and subscapular skinfolds) + 9.7

Males: %BF = 0.783 (sum of triceps and subscapular skinfolds) + 1.6

Slaughter 2: For subjects with sum triceps and subscapular skinfolds <35 mm

Females: %BF = 1.33 (sum of triceps and subscapular skinfolds) −0.013 (sum triceps and subscapular skinfolds)² −2.5

Males: 1.21 (sum of triceps and subscapular skinfolds) −0.008 (sum of triceps and subscapular skinfolds)² −3.4

Goran

%BF = (0.18 × weight + 0.23 × subscapular skinfolds + 0.13 × triceps skinfolds – 3) × 100/weight

Huang

%BF = [(0.764 × weight) – (0.471 × height) + 45.955] × 100/weight

BIA was performed with a portable device, the InBodyS10 multi-frequency United States. Electrodes are placed at eight precise tactile points of the body to achieve a multi-segmental frequency analysis. A total of 30 impedance measurements are obtained using six different frequencies 1, 5, 50, 250, 500, and 1000 kHz at the five following segments of the body: right and left arms, trunk, right and left legs. BIA was performed with the participant lying in the supine position on a nonconductive surface, with legs apart and arms held away from the body, with the least possible clothing, and without metal jewelry. Standard guidelines were followed for instructions to the subjects before BIA.²⁰ Each participant completed two evaluations, and the average of the two values was considered the result. All measurements were performed according to the manufacturer’s instructions with the use of the standardized technique by one of four experienced, trained researchers.

Statistical analysis

The Shapiro–Wilk test verified the normal distribution for all parameters. The results were presented as cases (proportion), mean ± standard deviation (SD), or by the median and interquartile range (P25-P75) for asymmetric distributions. The body composition data obtained by the two methods (BIA and skinfold thickness) were compared using Student’s t-test or the Mann–Whitney U test, when appropriate. The authors used the Bland–Altman graphical approach to verify the agreement between the methods and bias. A deviation up to 8% in the 95% limits of agreement (LOA) (relative bias within 1.96 × standard deviation) was considered clinically acceptable, considering the maximum variation expected for age group according to previous studies.^21,22

The data were analyzed using SPSS (v. 17.0; IBM Corporation – Armonk, New York, United States) and MedCalc Software (v. 12.1.4 – Ostend, Belgium). p-values below 0.05 were considered significant.

The study was approved by the Ethics Committee of Pontifícia Universidade Católica do Rio Grande do Sul, Brazil (CAAE: 48270515.3.1001.5336). Informed consent was obtained from the parents of the participants.

The sample size was determined using the Bland–Altman plot method. Considering a power of 80% and a level of significance of 0.05, expecting a mean difference of 5%, standard deviation of differences of 2%, and 10% maximum allowed difference between methods, 172 subjects were needed in the study.

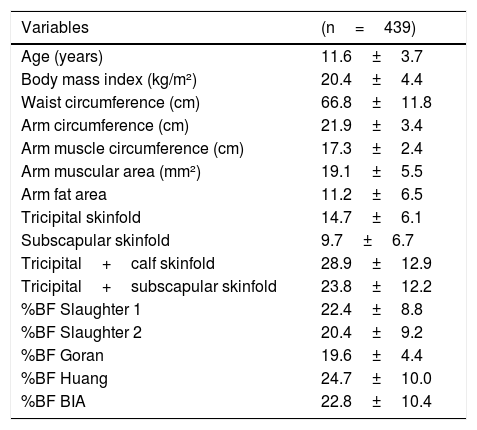
Results

A total of 439 subjects were evaluated, 144 (32.8%) children and 295 (67.2%) adolescents, with a mean age of 11.6 ± 3.7 years. There was a predominance of females (243, 55.4%) and self-declared whites (251, 65.9%). The mean weight was 47.0 ± 18.5 kg, BMI was 20.4 ± 4.4 kg/m², waist circumference was 66.8 ± 11.8 cm, arm circumference was 21.9 ± 3.4 cm, arm muscular area was 19.1 ± 5.5 mm², and area of arm fat was 11.2 ± 6.5 mm² (Table 1).

Table 1.

Descriptive values for anthropometric measurements and body composition.

Variables	(n = 439)
Age (years)	11.6 ± 3.7
Body mass index (kg/m²)	20.4 ± 4.4
Waist circumference (cm)	66.8 ± 11.8
Arm circumference (cm)	21.9 ± 3.4
Arm muscle circumference (cm)	17.3 ± 2.4
Arm muscular area (mm²)	19.1 ± 5.5
Arm fat area	11.2 ± 6.5
Tricipital skinfold	14.7 ± 6.1
Subscapular skinfold	9.7 ± 6.7
Tricipital + calf skinfold	28.9 ± 12.9
Tricipital + subscapular skinfold	23.8 ± 12.2
%BF Slaughter 1	22.4 ± 8.8
%BF Slaughter 2	20.4 ± 9.2
%BF Goran	19.6 ± 4.4
%BF Huang	24.7 ± 10.0
%BF BIA	22.8 ± 10.4

%BF, percentage body fat; BIA, bioimpedance analysis.

Values expressed as mean ± standard deviation.

The percentage of fat according to Slaughter 1 was 22.4% ± 8.8%, 20.4% ± 9.2% by Slaughter 2, 19.6% ± 4.4% by Goran, 24.7% ± 10.0% by Huang, and 22.8% ± 10.4% by BIA (Table 1).

When comparing the %BF by BIA with the estimates calculated using the equations, only Slaughter 1 and Huang demonstrated significant bias, with mean values of −1.71 (p = 0.015) and −1.68 (p < 0.001), respectively. However, the mean clinically acceptable lower and upper limits of agreement were higher than 8% for all equations (Fig. 1 and Supplementary Table S1). The results of the analysis by sex also demonstrated limits of agreement exceeding 8% for all equations (Supplementary Table S2).

Figure 1.

Bland–Altman plots illustrating the level of agreement between the bioelectrical impedance analysis (BIA) and Slaughter 1 (A), Slaughter 2 (B), Goran (C), and Huang (D) estimates of percent body fat. SD, standard deviation.

Discussion

The present study aimed to evaluate the agreement of four predictive equations based on the thickness of the skinfold and BIA in children and adolescents for the percentage of fat assessment. None of the equations had clinically acceptable agreement with BIA.

This variation, underestimating or overestimating the %BF, can be observed in other studies, independently of nutritional status.^10,12,23 It must considered that available equations are used worldwide have been developed in different populations, and most of them were only had good correlation with others measurement of body composition. Slaughter equations were developed in Illinois and replicated in Arizona, with 310 children, including four maturations groups of black and white children, adolescents, and adults.¹⁷ Huang’s equations were developed in the Hispanic population, with 96 children recruited in Los Angeles, United States, and with ages between 7 and 13 years.¹⁹ Goran’s equations were developed in Vermont and Arizona, with heterogeneous groups of 98 children aged 4–10 years.¹⁸ The authors also tested the correlation between the skinfolds thickness and BIA parameters. All skinfolds thickness parameters had a moderate correlation with BIA, and the equations (Slaughter 1, r² = 0.702; Slaughter 2, r² = 0.736; Goran, r² = 0.703; Huang, r² = 0.614; p < 0.001, respectively) confirmed earlier findings.^13,24–26 However, good correlation does not mean good agreement. Agreement is not something that can be interpreted with global indices, such as correlation coefficients, which do not help the clinician interpret a measurement, though they do have a place in the study of associated questions, such as the validity of measurement methods. Widely used statistical approaches, which the present authors believe are misleading, include correlation.²⁷

The potential limitations of this study should be considered. This study does not include a method that could be considered a gold standard, such as dual X-ray absorptiometry. However, given that dual X-ray absorptiometry requires exposure to radiation (albeit at a low dose), is high cost, and involves difficult transportation of the equipment and specific training, it is rarely used in clinical practice. However, a recent study in a Brazilian population confirmed the usefulness of BIA for predicting body composition.²⁸ The present study also used a multi-frequency, tetra-polar BIA with six measures of frequency, which allows the precise assessment of water balance and nutritional status.²⁹ The present study also did not include Tanner maturation assessment. However, as this study compared the same subject results with different techniques, it is believed that this limitation is unlikely to have significantly affected the results.

Despite the limitations, this study demonstrates that in clinical practice, none of the tested equations had good agreement with BIA. Considering that obesity increases the risk of developing chronic, non-transmissible disease in adulthood, which is associated with higher costs of medications, it is important to conduct an adequate nutritional and clinical assessment of children and adolescents. Also, this study included multiple ethnicities, urban and rural populations, and body types. Another important point of this study is the use of specific, multi-frequency BIA, which allows a detailed and precise assessment of the water balance and nutritional status.

Based on these findings, the authors conclude that skinfold thickness and BIA should not be used interchangeably in children and adolescents.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or non-profit sectors.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgments

Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES), Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), and Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul (FAPERGS).