Equations based on anthropometry to predict body fat measured by absorptiometry in schoolchildren and adolescents

Abstract

Objective

To develop and validate equations to estimate the percentage of body fat of children and adolescents from Mexico using anthropometric measurements.

Methods

A cross‐sectional study was carried out with 601 children and adolescents from Mexico aged 5–19 years. The participants were randomly divided into the following two groups: the development sample (n = 398) and the validation sample (n = 203). The validity of previously published equations (e.g., Slaughter) was also assessed. The percentage of body fat was estimated by dual‐energy X‐ray absorptiometry. The anthropometric measurements included height, sitting height, weight, waist and arm circumferences, skinfolds (triceps, biceps, subscapular, supra‐iliac, and calf), and elbow and bitrochanteric breadth. Linear regression models were estimated with the percentage of body fat as the dependent variable and the anthropometric measurements as the independent variables.

Results

Equations were created based on combinations of six to nine anthropometric variables and had coefficients of determination (r²) equal to or higher than 92.4% for boys and 85.8% for girls. In the validation sample, the developed equations had high r² values (≥85.6% in boys and ≥78.1% in girls) in all age groups, low standard errors (SE ≤ 3.05% in boys and ≤3.52% in girls), and the intercepts were not different from the origin (p > 0.050). Using the previously published equations, the coefficients of determination were lower, and/or the intercepts were different from the origin.

Conclusions

The equations developed in this study can be used to assess the percentage of body fat of Mexican schoolchildren and adolescents, as they demonstrate greater validity and lower error compared with previously published equations.

Resumo

Objetivo

Desenvolver e validar equações para estimar o percentual de gordura corporal (%GC) de crianças e adolescentes do México com medidas antropométricas.

Métodos

Foi feito um estudo transversal com 601 crianças e adolescentes do México cinco e 19 anos. Os participantes foram divididos aleatoriamente nos seguintes dois grupos: a amostra de desenvolvimento (n = 398) e a amostra de validação (n = 203). A validade das equações publicadas anteriormente (por exemplo, Slaughter) também foi avaliada. O %GC foi estimado por absorciometria de dupla energia de raios X (raios X de dupla energia [DXA]). As medidas antropométricas incluíram estatura, altura sentado, peso, circunferências da cintura e do braço, dobras cutâneas (tríceps, bíceps, subescapular, suprailíaca e panturrilha) e larguras do cotovelo e bitrocantérica. Os modelos de regressão linear foram estimados com o %GC, a variável dependente e as medidas antropométricas como as variáveis independentes.

Resultados

As equações foram criadas com base nas combinações de seis a nove variáveis antropométricas e apresentaram coeficientes de determinação (r²) iguais ou superiores a 92,4% para meninos e 85,8% para meninas. Na amostra de validação, as equações desenvolvidas apresentaram altos valores de r² (≥ 85,6% em meninos e ≥ 78,1% em meninas) em todos os grupos, baixo nível de erros padrão (EP ≤ 3,05% em meninos e ≤ 3,52% em meninas) e os interceptos não foram diferentes da origem (p > 0,050). Com as equações publicadas anteriormente, os coeficientes de determinação foram menores e/ou os interceptos foram diferentes da origem.

Conclusões

As equações desenvolvidas neste estudo podem ser usadas para avaliar o %GC das crianças em idade escolar e adolescentes mexicanos, pois têm uma maior validade e menor erro em comparação com as equações publicadas anteriormente.

Introdução

O sobrepeso e a obesidade são importantes questões de saúde pública devido à sua magnitude e a seu impacto sobre a saúde. Em 2012, a prevalência do sobrepeso e da obesidade em crianças em idade escolar no México entre cinco e 11 anos foi de 34,4% (19,8% e 14,6%, respectivamente) e em adolescentes entre 12 e 19 anos, de 34,9%.¹ Em crianças em idade escolar, esse valor foi ligeiramente maior (34,8%) em 2006, ao passo que em adolescentes foi menor (33,2%).

As crianças com obesidade tendem a se tornar adultos obesos, o que aumenta seu risco de desenvolvimento de doenças crônicas.² A obesidade representa um problema econômico, pois o tratamento de suas comorbidades envolve altos custos.³ Assim, é necessário que a obesidade seja diagnosticada de forma precisa.

Os diferentes métodos de avaliação da gordura corporal incluem hidrodensitometria, absorciometria de raios X de dupla energia (DXA) e diluição de deutério. Essas medidas são usadas principalmente em ambientes de pesquisa, pois os equipamentos necessários são caros e devem ser operados por técnicos especializados. Por esses motivos, esses métodos não são adequados para estudos populacionais, prática clínica e atividades de triagem. Pelo contrário, as medidas antropométricas, apesar de serem indicadores indiretos de adiposidade, são econômicas, invasivas e altamente reproduzíveis.⁴

Diferentes equações com base na antropometria têm sido usadas para estimar a gordura corporal em crianças e esses métodos foram desenvolvidos em indivíduos brancos e negros. As equações de Slaugther⁵ são as mais frequentemente usadas na avaliação da composição corporal em crianças e adolescentes.^6–9 Essas equações foram desenvolvidas em 310 pessoas negras e brancas de oito a 29 anos.⁵ Contudo, essas equações tendem a superestimar a gordura corporal.^8,9 Nos últimos anos, as equações de Dezenberg,⁷ que foram desenvolvidas em uma amostra de 202 crianças brancas entre quatro e 10 anos. Em crianças latinas dos Estados Unidos, essas equações estimam a gordura corporal de forma incorreta.¹⁰ Esses resultados mostram que as equações desenvolvidas em um grupo étnico podem ser usadas em outras populações, porém a estimativa obtida pode ser imprecisa. No caso da população latina, foi reconhecido que a população mexicana atual é uma mistura entre descendentes ameríndios, europeus e africanos.¹¹

Poucos estudos na América Latina exploraram a validade das equações de predição para estimar a gordura corporal em crianças com medidas antropométricas.^12,13 É possível que as equações desenvolvidas nas populações de ancestrais europeus e africanos não possam ser aplicadas a populações latino‐americanas devido a diferenças étnicas na quantidade e distribuição de gordura corporal. Por exemplo, em comparação com crianças brancas ou negras, aquelas com ancestrais latinos têm maior circunferência da cintura.¹⁴ Além disso, as populações pediátricas latino‐americanas têm maior peso com relação à sua estatura (um indicador indireto de adiposidade), que nem sempre se deve ao excesso de gordura corporal.^15,16 Outros motivos de peso elevado sem excesso de adiposidade podem ser que, em comparação com a população de referência, as populações latinas são mais baixas,^15,16 porém têm maiores valores de massa muscular,¹⁶ hidratação da massa livre de gordura,¹⁷ comprimento do tronco,¹⁵ estrutura corporal (ou seja, espessura óssea)¹⁵ e circunferência torácica.¹⁸ Portanto, os objetivos deste estudo foram: 1) avaliar a validade das equações publicadas anteriormente para estimar o %GC em crianças latinas e 2) desenvolver e validar novas equações em crianças latinas para prever a gordura corporal com o DXA como padrão de base.

Métodos

Foi feito um estudo transversal com uma amostra de conveniência de crianças em idade escolar e adolescentes entre cinco e 19 anos da Cidade do México. Os participantes foram recrutados da escola primária (n = 7), do ensino fundamental (n = 8) e do colegial (n = 4) na Cidade do México e de um centro comunitário no Estado do México. A equipe de pesquisa apresentou o projeto para o diretor de cada escola e todos os estudantes foram convidados a participar. Além disso, as crianças de funcionários da Universidade Autônoma Metropolitana de Xochimilco (UAM‐X) participaram do estudo. As crianças com gesso ou incapacidades motoras foram excluídas. O estudo foi aprovado pelo Departamento de Ciências Biológicas e da Saúde da UAM‐X. Os participantes e seus pais ou responsáveis foram informados dos procedimentos da pesquisa e, posteriormente, forneceram o consentimento informado.

De acordo com os procedimentos usados em outros estudos,^7,10,19 a amostra total (n = 601) foi dividida aleatoriamente em dois grupos. Os dados de 2/3 dos participantes foram usados para desenvolver equações (n = 398) e os dados do restante de 1/3 das crianças foram usados para validar novas equações e as publicadas anteriormente (n = 203). O pacote de software SPSS (IBM Corp. 2010. IBM SPSS Statistics para Windows, versão 20.0. NY, EUA) foi usado para gerar essas amostras (opção “Amostra aleatória de casos” no comando “Seleção de casos”).

A maior parte das medidas antropométricas foi obtida de acordo com as técnicas descritas por Lohman et al.²⁰ A circunferência da cintura foi medida de acordo com a técnica descrita por Fernández et al.¹⁴ Os analistas foram padronizados de acordo com o protocolo de Habicht.²¹ Os participantes foram medidos com roupas leves e sem sapatos. A estatura foi medida com um estadiômetro portátil modelo 214 (SECA®, SP, Brasil) e o peso corporal com uma balança digital modelo 813 (SECA®, SP, Brasil). As circunferências da cintura e do braço foram obtidas com uma fita metálica (Lufkin®, MD, EUA). As dobras cutâneas (do tríceps, bicipital, subescapular, suprailíaca e da panturrilha) foram medidas com um compasso (Harpenden®, Mediflex Produtos Cirúrgicos, NY, EUA). Cada dobra cutânea foi medida três vezes e foi analisado seu valor médio. A largura bitrocantérica e a altura sentada foram obtidas com um antropômetro (Harpenden®, Mediflex Produtos Cirúrgicos, NY, EUA). A largura do cotovelo foi medida com um antropômetro (Futrex®, MD, EUA).

O índice de massa corporal (IMC: peso corporal/altura²) foi calculado como escore Z para idade e sexo com o uso da referência da Organização Mundial de Saúde.²² A maturação foi estimada com as equações de Mirwald et al.²³

O percentual de gordura corporal (%GC) foi avaliado com absorciometria de dupla energia de raios X (DXA) com os equipamentos modelo Discovery Wi (Hologic®, MA, EUA). A calibragem, digitalização e análise das imagens foram concluídas de acordo com os procedimentos do fabricante e os descritos pela Sociedade Internacional de Densitometria Clínica (ISCD).²⁴ As imagens foram analisadas com a opção de corpo inteiro da população hispânica, modelo APEX versão 3.3.0.1 (Hologic®, MA, EUA). Os coeficientes de variação do técnico foram 1,27% para gordura corporal total (GCT) em quilogramas, 0,66% para massa corporal magra e 1,04% para GCT, que são aceitáveis de acordo com a ISCD.²⁴

A distribuição das variáveis antropométricas foi avaliada com o teste de Kolmogorov‐Smirnov (tabela 1). Quando a variável apresentou uma distribuição enviesada, ela foi transformada com a base logarítmica 10 para atingir uma distribuição simétrica mais próxima. Os modelos de regressão linear foram estimados com a DXA derivada do %GC como uma variável dependente e a medida antropométrica como variáveis independentes. Modelos separados foram estimados para sexo. As equações foram desenvolvidas com os dois seguintes procedimentos:

Tabela 1.

Estatísticas descritivas das medidas antropométricas nas amostras de desenvolvimento e validação de crianças e adolescentes mexicanos

	Amostra de desenvolvimento		Amostra de validação
	Meninos (n = 191)	Meninas (n = 207)	Meninos (n = 100)	Meninas (n = 103)
	% (n)	% (n)	% (n)	% (n)
Maturação sexual
Pré‐puberdade	66,0 (126)	30,9 (64)	75,0 (75)	42,7 (44)
Puberdade	27,2 (52)	38,6 (80)	22,0 (22)	34,0 (35)
Pós‐puberdade	6,8 (13)	30,4 (63)	3,0 (3)	23,3 (24)

	Média ± DP	Média ± DP	Média ± DP	Média ± DP
Gordura corporal (%)	27,1 ± 9,4	32,6 ± 7,0	25,8 ± 9,0	32,8 ± 7,4
Idade (anos)	11,3 ± 2,7	11,5 ± 2,9	10,9 ± 2,6	10,9 ± 2,9
Idade^2(anos^2)	136,0 ± 59,2^a	141,1 ± 67,5^a	133,3 ± 56,0	127,9 ± 62,6
Estatura (cm)	149,2 ± 16,9	146,2 ± 13,1^c	144,2 ± 15,3	145,2 ± 13,7
Altura sentado (cm)	76,9 ± 8,1	76,5 ± 7,2^b	74,3 ± 7,5	75,5 ± 7,9
Índice de altura sentado (%)	51,7 ± 1,8^a	52,3 ± 1,9	51,6 ± 2,6	52,0 ± 2,7^a
Peso (kg)	47,4 ± 15,9	45,0 ± 14,2	42,0 ± 14,3	43,7 ± 14,0
Índice de massa corporal (kg/m^2)	20,7 ± 4,2	20,5 ± 4,1	19,7 ± 3,8	20,3 ± 4,3
Circunferência do braço (cm)	24,2 ± 4,1	23,9 ± 3,8	23,2 ± 3,8	23,9 ± 3,7
Circunferência da cintura (cm)	73,8 ± 12,9	72,0 ± 11,2	70,1 ± 11,4	72,5 ± 10,8
Dobra cutânea do tríceps (mm)	14,9 ± 6,6^a	16,7 ± 5,5	14,2 ± 6,3	17,2 ± 5,8
Sobra cutânea do bíceps (mm)	8,3 ± 4,5^c	9,0 ± 3,9^a	7,7 ± 3,8^a	9,8 ± 4,8^a
Dobra cutânea subescapular (mm)	14,2 ± 7,8^a	15,7 ± 7,2	13,0 ± 7,6^b	16,0 ± 9,2
Dobra cutânea suprailíaca (mm)	18,9 ± 12,7^a	22,0 ± 12,0	16,0 ± 11,3^a	21,9 ± 11,9
Sobra cutânea da panturrilha (mm)	14,1 ± 6,7^a	15,8 ± 6,5	12,4 ± 5,9^a	16,0 ± 6,6
Largura bitrocortérica (cm)	29,7 ± 4,9	29,5 ± 4,2	27,9 ± 4,4	29,3 ± 4,5
Largura do cotovelo (cm)	5,6 ± 0,6	5,1 ± 0,4	5,4 ± 0,6	5,1 ± 0,4

Significância no teste de Kolmogorov‐Smirnov:

a

p ≤ 0,050.

b

p ≤ 0,010.

c

p ≤ 0,001.

a) As diferentes combinações de variáveis independentes foram testadas manualmente. Primeiro, foi avaliada a capacidade de cada variável antropométrica estimar o %GC (Tabela Complementar 1). Além disso, os gráficos de dispersão foram grafados para verificar a relação linear entre as variáveis. Uma relação curvilínea do %GC com a idade foi evidente nos meninos; ao passo que, entre as meninas, essa relação foi linear. Por esse motivo, nos modelos para meninos, foi incorporado o termo quadrático da idade. Como a idade e a maturação estão relacionadas, foram estimados modelos separados com cada variável e nenhuma diferença foi observada. Para simplicidade, foram relatados apenas modelos com idade. O coeficiente de determinação (r²) e o erro padrão (EP) foram usados como critérios para identificar as variáveis que melhor predizem o %GC. Uma variável foi considerada um preditor adequado quando o valor de p< 0,050.

b) Foram usados os procedimentos automáticos backward e forward do comando “regressão linear” do software SPSS (tabela 2). Na opção backward, todas as variáveis foram introduzidas nos modelos e, então, aqueles que apresentaram uma baixa correlação parcial com a variável dependente foram excluídos (critérios de eliminação: p > 0.100). Na opção forward, as variáveis foram introduzidas uma por uma de acordo com a maior correlação com a variável dependente. Essas variáveis foram introduzidas e mantidas caso fossem preditoras significativas da variável dependente (p < 0,050).

Tabela 2.

Modelos de regressão linear múltipla com %GC pela DXA como resultado e características antropométricas como preditores na amostra de desenvolvimento de crianças e adolescentes mexicanos

Equações	Modelos de regressão linear múltipla	r^2 (%)	EP (%)
Para meninos
1	−8,739 ‐ 0.384^c (estatura, cm) + 35,371^a (peso registrado, kg) – 0,892^b (IMC, kg/m^2) – 0,299^a (circunferência do braço, cm) + 0,258^c (circunferência da cintura, cm) + 17,732^c (registro da dobra cutânea do tríceps) + 6,698^b (registro da dobra cutânea subescapular) + 3,545^d (registro da dobra cutânea suprailíaca) + 4,019^d (registro da dobra cutânea da panturrilha)	93,4	2,5
2	1,511 – 0,152^c (estatura, cm) – 0,431^c (circunferência do braço, cm) + 0,213^c (circunferência da cintura, cm) + 21,271^c (registro da dobra cutânea do tríceps) + 7,386^b (registro da dobra cutânea subescapular) + 4,981^b (registro da dobra cutânea suprailíaca)	92,7	2,56
3	−1,791 + 0,329 (idade, anos) – 0,033^a (idade^2, anos^2) – 0,141^c (estatura, cm) + 0,162^c (circunferência da cintura, cm) + 18,516^c (registro da dobra cutânea do tríceps) + 6,013^a (registro da dobra cutânea subescapular) + 5,633^b (registro da dobra cutânea suprailíaca)	92,4	2,61
Para meninas
1	−7,299 ‐ 21,436^b (registro altura sentado) + 17,739^b (registro do IMC) + 20,143^a (circunferência da cintura) + 7,813^c (registro da dobra cutânea do tríceps) + 6,379^b (registro da dobra cutânea subescapular) + 6,051^b (registro da dobra cutânea da panturrilha) – 16,364^a (registro da largura do cotovelo)	85,8	2,65

%GC pela DXA, percentual de gordura corporal estimada pela absorciometria de dupla energia de raios X; EP, erro padrão; IMC, índice de massa corporal.

Os valores de p dos coeficientes de regressão foram:

a

p < 0,050.

b

p < 0,010.

c

p < 0,001.

d

p ≤ 0,072.

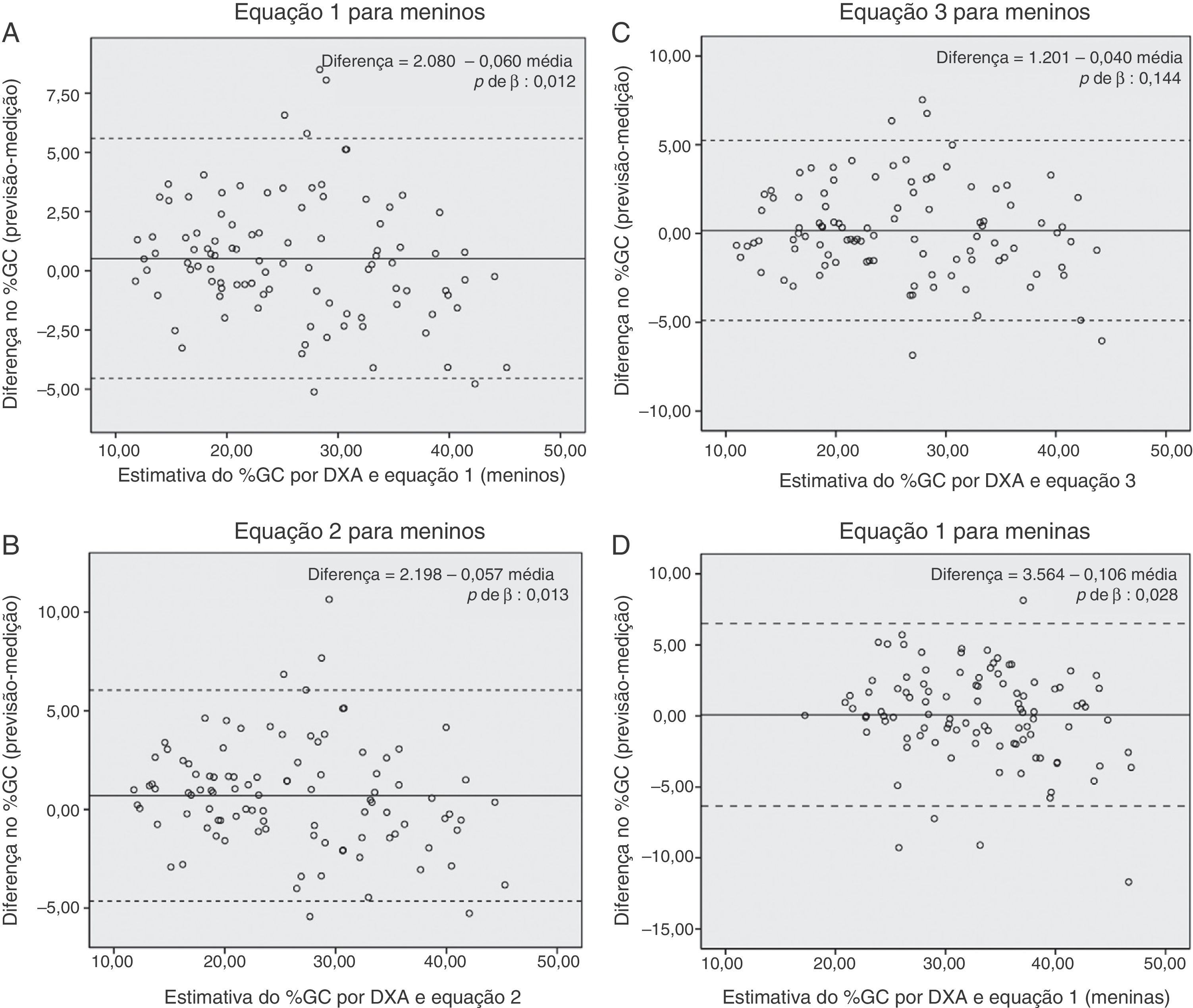
A avaliação da validade das equações publicadas anteriormente foi feita com indivíduos com idades compatíveis da população que foi usada para desenvolvê‐las (por exemplo, para as equações de Slaughter²⁵ foram usados os dados dos participantes entre oito e 18 anos e para as equações de Deurenberg²⁶ a idade foi entre sete e 19 anos). A validade das equações de Stevens para meninas não pôde ser avaliada devido à falta de dados das crianças em idade de menarca. Nesses modelos de regressão, a variável dependente foi a DXA derivada do %GC e a variável independente foi o %GC obtido pelas equações desenvolvidas anteriormente e aquelas desenvolvidas neste estudo (tabela 3). Um critério para a validade foi se houve uma diferença significativa entre o intercepto e a origem (p > 0,050), pois, caso haja diferença, as equações superestimariam ou subestimariam sistematicamente o %GC. Por fim, os gráficos de Bland Altman foram grafados (fig. 1 e Figura Complementar 1) para verificar a existência de viés nas estimativas de acordo com os níveis de adiposidade. As diferenças entre o %GC medido e estimado foram traçadas com relação à média de %GC medido e estimado. Apenas as equações cujo intercepto não foi diferente da origem foram traçadas. As análises estatísticas foram feitas com o software SPSS (IBM Corp. 2010. IBM SPSS Statistics para Windows, Versão 20.0. NY, EUA).

Tabela 3.

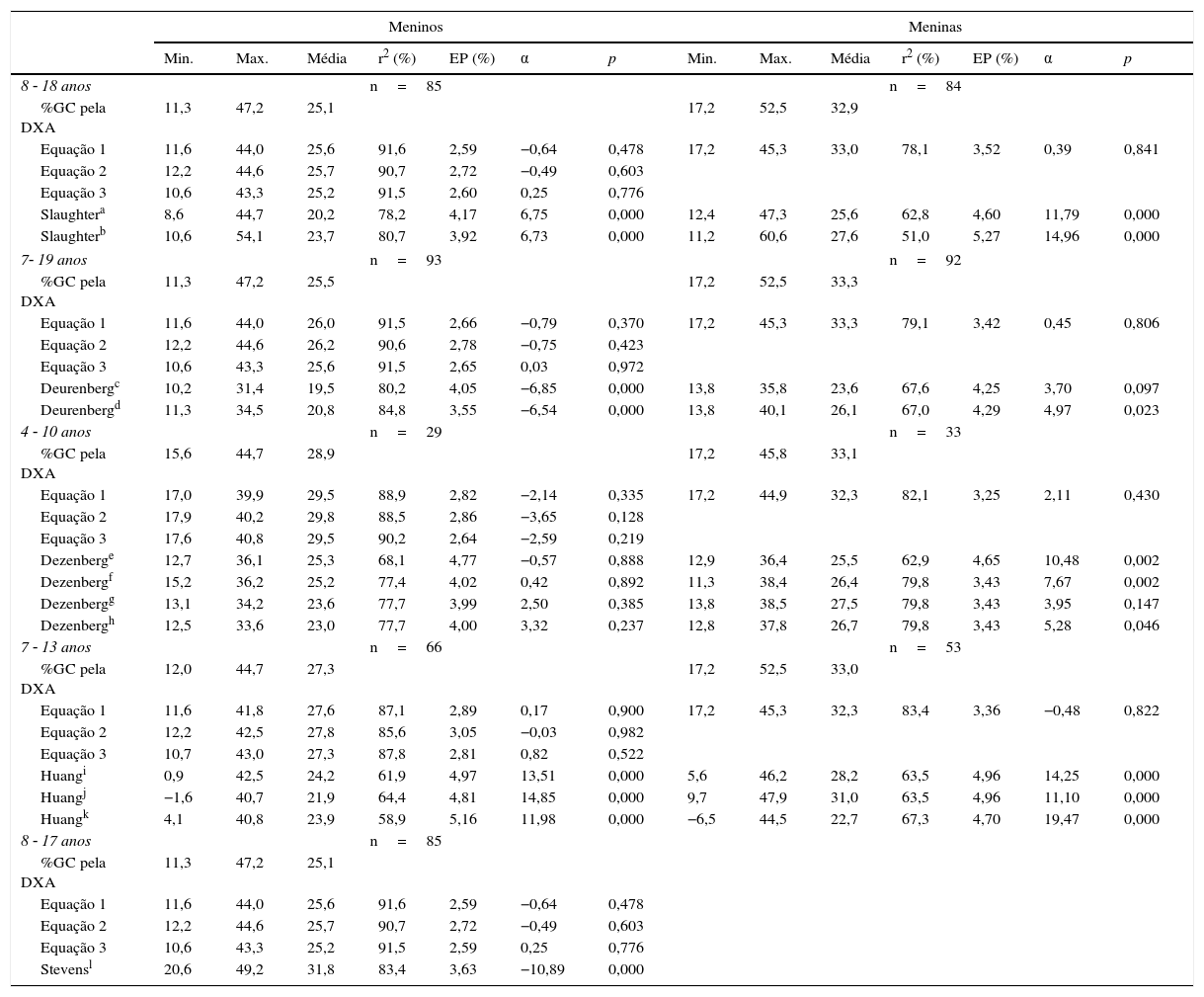
Validação cruzada das novas equações e das equações publicadas anteriormente na amostra de validação de crianças e adolescentes mexicanos

	Meninos							Meninas
	Min.	Max.	Média	r^2 (%)	EP (%)	α	p	Min.	Max.	Média	r^2 (%)	EP (%)	α	p
8 ‐ 18 anos	n = 85							n = 84
%GC pela DXA	11,3	47,2	25,1					17,2	52,5	32,9
Equação 1	11,6	44,0	25,6	91,6	2,59	−0,64	0,478	17,2	45,3	33,0	78,1	3,52	0,39	0,841
Equação 2	12,2	44,6	25,7	90,7	2,72	−0,49	0,603
Equação 3	10,6	43,3	25,2	91,5	2,60	0,25	0,776
Slaughter^a	8,6	44,7	20,2	78,2	4,17	6,75	0,000	12,4	47,3	25,6	62,8	4,60	11,79	0,000
Slaughter^b	10,6	54,1	23,7	80,7	3,92	6,73	0,000	11,2	60,6	27,6	51,0	5,27	14,96	0,000
7‐ 19 anos	n = 93							n = 92
%GC pela DXA	11,3	47,2	25,5					17,2	52,5	33,3
Equação 1	11,6	44,0	26,0	91,5	2,66	−0,79	0,370	17,2	45,3	33,3	79,1	3,42	0,45	0,806
Equação 2	12,2	44,6	26,2	90,6	2,78	−0,75	0,423
Equação 3	10,6	43,3	25,6	91,5	2,65	0,03	0,972
Deurenberg^c	10,2	31,4	19,5	80,2	4,05	−6,85	0,000	13,8	35,8	23,6	67,6	4,25	3,70	0,097
Deurenberg^d	11,3	34,5	20,8	84,8	3,55	−6,54	0,000	13,8	40,1	26,1	67,0	4,29	4,97	0,023
4 ‐ 10 anos	n = 29							n = 33
%GC pela DXA	15,6	44,7	28,9					17,2	45,8	33,1
Equação 1	17,0	39,9	29,5	88,9	2,82	−2,14	0,335	17,2	44,9	32,3	82,1	3,25	2,11	0,430
Equação 2	17,9	40,2	29,8	88,5	2,86	−3,65	0,128
Equação 3	17,6	40,8	29,5	90,2	2,64	−2,59	0,219
Dezenberg^e	12,7	36,1	25,3	68,1	4,77	−0,57	0,888	12,9	36,4	25,5	62,9	4,65	10,48	0,002
Dezenberg^f	15,2	36,2	25,2	77,4	4,02	0,42	0,892	11,3	38,4	26,4	79,8	3,43	7,67	0,002
Dezenberg^g	13,1	34,2	23,6	77,7	3,99	2,50	0,385	13,8	38,5	27,5	79,8	3,43	3,95	0,147
Dezenberg^h	12,5	33,6	23,0	77,7	4,00	3,32	0,237	12,8	37,8	26,7	79,8	3,43	5,28	0,046
7 ‐ 13 anos	n = 66							n = 53
%GC pela DXA	12,0	44,7	27,3					17,2	52,5	33,0
Equação 1	11,6	41,8	27,6	87,1	2,89	0,17	0,900	17,2	45,3	32,3	83,4	3,36	−0,48	0,822
Equação 2	12,2	42,5	27,8	85,6	3,05	−0,03	0,982
Equação 3	10,7	43,0	27,3	87,8	2,81	0,82	0,522
Huang^i	0,9	42,5	24,2	61,9	4,97	13,51	0,000	5,6	46,2	28,2	63,5	4,96	14,25	0,000
Huang^j	−1,6	40,7	21,9	64,4	4,81	14,85	0,000	9,7	47,9	31,0	63,5	4,96	11,10	0,000
Huang^k	4,1	40,8	23,9	58,9	5,16	11,98	0,000	−6,5	44,5	22,7	67,3	4,70	19,47	0,000
8 ‐ 17 anos	n = 85
%GC pela DXA	11,3	47,2	25,1
Equação 1	11,6	44,0	25,6	91,6	2,59	−0,64	0,478
Equação 2	12,2	44,6	25,7	90,7	2,72	−0,49	0,603
Equação 3	10,6	43,3	25,2	91,5	2,59	0,25	0,776
Stevens^l	20,6	49,2	31,8	83,4	3,63	−10,89	0,000

α, intercepto; %GC pela DXA, percentual de gordura corporal estimada pela absorciometria de dupla energia de raios X; B‐SF, dobra cutânea do bíceps; C‐SF, dobra cutânea da panturrilha; EP, erro padrão; Max, Máximo; Min, mínimo; r², coeficiente de determinação; SI‐SF, dobra cutânea suprailíaca; SS‐SF, dobra cutânea subescapular; T‐SF, dobra cutânea do tríceps;

As estimativas foram feitas com base:

a

T‐SF e C‐SF.

b

T‐SF e SS‐SF.

c

T‐SF e B‐SF.

d

T‐SF, B‐SF SI‐SF e SS‐SF.

e

Peso.

f

Peso e T‐SF.

g

Peso, T‐SF e sexo.

h

Peso, T‐SF, sexo e etnia.

i

Idade.

j

Idade e sexo.

k

Idade, sexo e altura.

l

Idade, etnia, peso, altura, cintura e T‐SF.

Figura 1.

Gráficos de Bland‐Altman para diferença no %GC medido pela DXA e estimativa do %GC por novas equações preditivas com base na antropometria na amostra de validação de crianças e adolescentes mexicanos. %GC pela DXA, percentual de gordura corporal estimada pela absorciometria de dupla energia de raios X.

A análise de poder estatístico para diferentes cenários foi concluída com o software G*Power.²⁷ Para o desenvolvimento de equações (tabela 2) considerando um nível de significância (α) de 0,050, um tamanho da amostra de 207, um efeito de 85,8% (r²) e sete preditores (cenário de equação para as meninas), o poder estatístico foi 1,00. O mesmo resultado foi obtido com o cenário das três equações para os meninos. Para a análise de validação (tabela 3), o poder obtido de acordo com os diferentes cenários a respeito do tamanho da amostra (n de 29 a 93), do efeito (r² de 51,0 a 91,6%) e do número de preditores (1 a 7) sempre foi satisfatório (ou seja, ≥ 0,80).

Resultados

Uma análise descritiva das variáveis antropométricas nas amostras de desenvolvimento e validação é apresentada na tabela 1. A idade média na amostra de desenvolvimento foi 11,88 anos, que está acima da amostra de validação (11,32 anos, p = 0,019). Em ambas as amostras, metade dos participantes era menina (amostra de desenvolvimento: 52%, amostra de validação: 50,7%). Apesar de a maior parte dos participantes estar na fase pré‐púbere, a proporção foi maior na amostra de validação do que na amostra de desenvolvimento (58,6% em comparação com 47,7%, p = 0,050).

Para cada grupo sexual, as diferentes características antropométricas estavam relacionadas ao %GC (Tabela Complementar 1). Nos meninos, as variáveis que mais bem predisseram o %GC foram idade, estatura, IMC, circunferências do braço e cintura, larguras bitrocortérica e do cotovelo, altura sentado, peso, índice de altura sentado e cinco dobras cutâneas. Entre as meninas, os melhores preditores foram idade, estatura, peso, altura sentado, índice de altura sentado, IMC, circunferência do braço e da cintura, cinco dobras cutâneas e larguras bitrocortérica e do cotovelo.

Com procedimentos automáticos, os dois modelos predisseram satisfatoriamente o %GC em meninos (tabela 2). Com a opção backward, as seguintes variáveis foram incluídas no modelo (chamado de equação 1): estatura, IMC, circunferências do braço e da cintura, peso corporal e dobras cutâneas do tríceps, subescapular, suprailíaca e da panturrilha (r² = 93%, EP = 2,5%). Com a opção forward, o modelo (chamado de equação 2) incluiu as seguintes variáveis: estatura, circunferências do braço e da cintura e dobras cutâneas do tríceps, subescapular e suprailíaca (r² = 92%, EP = 2,5%). Nos meninos, a seleção manual produziu um modelo (equação 3) que incluiu idade, estatura, circunferência da cintura e dobras cutâneas do tríceps, subescapular e suprailíaca (r² = 92%, EP = 2,0%). Nas meninas, ambos os procedimentos automáticos produziram a mesma solução (chamada de equação 1) com as seguintes variáveis: altura sentado, IMC, circunferência da cintura, largura do cotovelo e dobras cutâneas do tríceps, subescapular e da panturrilha (r² = 85%, EP = 2,5%). Entre as meninas, o modelo de seleção manual não predisse adequadamente o %GC (r² ≥ 80,0%).

A tabela 3 mostra as diferentes estimativas do %GC obtidas pelas equações na amostra de validação. Em todas as faixas etárias, as equações recém‐desenvolvidas em crianças em idade escolar e adolescentes mexicanos apresentaram altos coeficientes de determinação (r² ≥ 85% em meninos e ≥ 78% em meninas) e o menor EP (≤ 3,05% em meninos e ≤ 3,52% em meninas); além disso, seus interceptos não diferiram da origem (p > 0,050). Apesar de, com as equações de Dezenberg, o intercepto não ter diferido da origem (p > 0,050), sua capacidade preditora (r² ≥ 77,7 em meninos e < 79,8 em meninas) foi inferior à das equações desenvolvidas aqui (r² ≥ 88 e 82%, respectivamente). As equações de Stevens, nos meninos, explicou uma proporção significativa de variância (r² = 85%), porém o intercepto diferiu da origem. Em ambos os sexos, as equações de Slaugther superestimaram o %GC (intercepto positivo, p < 0,050). As equações de Deurenberg subestimaram o %GC nos meninos (intercepto negativo, p < 0,050) e superestimaram nas meninas. As equações de Huang superestimaram o %GC em ambos os sexos.

Os gráficos de Bland‐Altman (fig. 1A, B e D) revelaram que as equações desenvolvidas por meio de procedimentos automáticos produzem estimativas enviesadas do %GC. Essas equações superestimaram valores nas crianças com baixa adiposidade, ao passo que, naquelas com alta adiposidade, os valores são subestimados. A equação desenvolvida por seleção manual nos meninos produziu estimativas sem viés sistemático (fig. 1C).

Discussão

O principal objetivo deste estudo foi desenvolver equações com base nas medidas antropométricas para prever o %GC de crianças em idade escolar e adolescentes mexicanos. As quatro equações desenvolvidas exigem medidas relacionadas à adiposidade, ao crescimento linear e à estrutura corporal. Para os meninos, três equações explicaram uma alta proporção da variância do %GC (r² ≥ 92%). Apesar de a equação, para as meninas, ter explicado uma alta proporção de variância (85%), ela foi menor do que a dos meninos. Outro objetivo do estudo foi analisar a validade das equações desenvolvidas anteriormente. Com exceção das equações de Dezenberg, nenhuma das equações publicadas anteriormente foi válida na amostra de crianças em idade escolar e adolescentes mexicanos.

Em sua população original,⁵ as equações de Slaugther tinham capacidade preditora aceitável (r² de 75% a 78% na amostra total). Contudo, nas crianças em idade escolar e adolescentes mexicanos, essas equações superestimaram o %GC. A mesma tendência foi observada em crianças indianas,⁹ crianças chinesas com obesidade⁸ e crianças britânicas.⁶ As equações de Deurenberg²⁶ foram desenvolvidas em 379 crianças e adolescentes holandeses entre sete e 20 anos e tinham capacidade preditora baixa a moderada (r² = 41% a 69% na amostra total). Na população pediátrica mexicana, essas equações subestimaram o %GC nos meninos e superestimaram nas meninas. Contudo, ocorreu o efeito oposto nas crianças britânicas.⁶ As diferenças físicas das crianças e adolescentes mexicanos em comparação com as que participaram dos estudos de Slaughter²⁵ e Deurenberg²⁶ podem explicar os resultados encontrados neste estudo. Os participantes nas amostras de Slaughter²⁵ e Deurenberg²⁶ eram mais altos (155,2 cm e 164,3 cm em comparação com 144,2 cm, respectivamente) e mais pesados (47,4 kg e 53,9 kg em comparação com 42 kg, respectivamente) do que as crianças na amostra mexicana, porém tinham menor %GC (16,7% e 15,1% em comparação com 25,8%, respectivamente).

Nas crianças em idade escolar e adolescentes mexicanos, as estimativas obtidas com as equações de Dezenberg não tendem a superestimar ou subestimar sistematicamente o %GC (ou seja, o intercepto não difere da origem). Contudo, a capacidade preditora das equações de Dezenberg (r² = 68,1% a 77,4% nos meninos e 62,9% a 79,8% nas meninas) foi inferior à das equações desenvolvidas neste estudo (88,5% a 90,2% e 82,1%, respectivamente). Achados semelhantes foram obtidos nas crianças em idade escolar em Cuba.²⁸ Contudo, nas crianças em idade escolar latinas¹⁰ e indianas,⁹ as equações de Dezenberg subestimaram o %GC; ao passo que, nas crianças em idade escolar do Reino Unido, essas equações apresentaram um viés de 13% na estimativa do %GC medido por diluição de deutério.²⁹

As equações de Huang¹⁰ foram desenvolvidas em crianças em idade escolar latinas entre sete e 13 anos nos Estados Unidos e tinham uma capacidade preditora aceitável (r² = 86% a 97% na amostra total). Na amostra mexicana, essas equações superestimaram o %GC. Apesar de os participantes do estudo de Huang serem latinos, eles eram mais pesados do que as crianças em idade escolar do México em nossa amostra. Essas diferenças podem refletir os diferentes cenários nos quais vivem as crianças americanas e mexicanas.

As equações de Stevens¹⁹ foram desenvolvidas com uma amostra multiétnica de 5.374 indivíduos entre oito e 17 anos e tinham uma capacidade preditiva de até 85% nos meninos, com a DXA como o padrão de base. Essa equação mostrou tendência de subestimar o %GC nas crianças em idade escolar e adolescentes mexicanos.

A população latino‐americana tem certas características físicas, como estatura mais baixa, extremidades inferiores curtas, maiores níveis de gordura corporal no tronco e nas regiões abdominais e estrutura corporal maior.^14–16 Por esse motivo, no presente estudo, as características corporais relacionadas ao crescimento linear (ou seja, estatura ou altura sentado) e à estrutura corporal (ou seja, larguras do cotovelo e bitrocortérica) foram medidas além das relacionadas à adiposidade (ou seja, dobras cutâneas e circunferências da cinturas). Nas equações desenvolvidas para meninos, a estatura apresentou um coeficiente de regressão negativo; ao passo que nas meninas, os coeficientes da largura do cotovelo e o índice de altura sentado também foram negativos. Isso mostra que as crianças ou adolescentes com maior estatura ou maior estrutura corporal tendem a ter menos adiposidade. Além disso, as novas medições pelas equações da gordura abdominal e do tronco foram preditores do %GC, incluindo a circunferência da cintura e as dobras cutâneas subescapular e suprailíaca.

Uma limitação do estudo é que foi usada uma amostra conveniente. Portanto, a generalização de nossos achados deve ser feita com cautela. Outra limitação é que, apesar de a DXA ser considerada um método adequado para medir a adiposidade,³⁰ sua validade em uma população mexicana não foi estabelecida. No desenvolvimento das equações para crianças e adolescentes mexicanos, uma capacidade menos preditiva foi observada nas meninas do que nos meninos. Essa diferença no sexo foi observada em outras amostras.^19,26 No futuro, as medições devem ser identificadas de forma a aumentar a capacidade preditiva das equações para as meninas. Uma importante limitação desta pesquisa é que usamos uma amostra de conveniência de crianças e adolescentes da Cidade do México, e, portanto, a amostra tem uma composição étnica específica. Dessa forma, apesar de as equações desenvolvidas fornecerem uma estimativa aprimorada do %GC na amostra em estudo, seu uso em outras populações deve ser cauteloso. Em outras palavras, nossas equações devem ser avaliadas em outras amostras de crianças de outras regiões do México e de outros países da América Latina. Isso é necessário, pois a população latino‐americana é diversa em termos de descendência étnica. Por exemplo, na região Sudeste do México, há uma predominância da descendência ameríndia na Europa, ao passo que na região Norte a tendência é o oposto.¹¹ Por fim, deve ser determinada a capacidade preditiva da estimativa do %GC (com as equações publicadas aqui) para identificar os resultados clinicamente relevantes (ou seja, riscos cardiovasculares).

Conclusão: nossos achados indicam que as equações desenvolvidas com base nas medidas antropométricas predizem adequadamente o %GC em um grupo heterogêneo de crianças em idade escolar e adolescentes mexicanos. Em contrapartida, as equações desenvolvidas em outras populações (mesmo com características étnicas semelhantes) reduziram a capacidade preditiva de estimar o %GC. Portanto, as equações desenvolvidas neste estudo podem ser usadas para avaliar o %GC das crianças em idade escolar e adolescentes mexicanos, pois elas têm uma maior validade e menor erro em comparação às equações publicadas anteriormente.

Conflitos de interesse

Os autores declaram não haver conflitos de interesse.

Agradecimentos

A Magdalena Rodriguez‐Magallanes – da Unidade de Nutrição, Composição Corporal e Gasto Calórico – que padronizou os analistas que fizeram as medidas antropométricas.